Fraction – Skill required
· Addition and subtraction of like and unlike fractions
· Recognising mixed numbers and improper fractions and able to convert improper fractions to mixed numbers and vice versa.
· Understanding fractions of a set ( Multiplying whole numbers by fractions.
· Solving word problems involving fractions involving adding, subtracting and multiplying.
Problem Solving
1. A florist had some roses in her shop. 1/6 of the roses were sold in the morning and 1/3 of them sold in the afternoon. If 66 roses were left, how many roses were in the shop at first?
2. Kumar has 7/11 as many stamps as Ali. If Ali gives Kumar 18 stamps, both of them will have an equal number of stamps. How many stamps do they have altogether?
3. Mr Lim had 16 guppies. He gave 3/8 of them to his daughter.
a. What fraction of the fish had he left?
b. How many guppies had he left?
4. Mandy had 3/7 of the number of beads that Jenny had at first. When Mandy received 22 beads from Jenny, both of them would have an equal number of beads.
a. How many more beads did Jenny have than Mandy at first?
b. How many beads did they have altogether?
5. James had a certain number of bookmarks. He gave ¾ of the bookmarks to his brother. James and Benny then shared the remaining number of bookmarks equally. Given that James had 46 bookmarks at the end, how many bookmarks did he have at first?
6. Jon bought 3 identical shirts and 4 identical belts for $130. If each belt cost 1/3 as much as a shirt, find the cost of a shirt.
7. Mary has 1/9 as many paper clips as John. John has 144 paper clips more than Mary. How many paper clips must John give Mary so that they will have the same number of paper clips?
8. 3/8 of the pupils in a class like English. 3/5 of the remaining pupils like Maths and the rest like Science. If 9 pupils like Science, how many pupils are there in the class?
9. There are 240 flowers in a garden. 1/5 of the flowers are daisies and 3/8 of the flowers are tulips. The rest are sunflowers. If 1/3 of the daisies and 5/6 of the tulips are removed, how many flowers will be left in the garden?
10. 2/5 of the colored paper in the packet are yellow. 0.5 of them are purple. The remaining ones are green. If there are 60 fewer green colored paper than the purple ones, how many colored paper does the packet contain altogether?
11. A baker sold 2/3 of his breads in the morning. He sold 1/6 of them in the afternoon. He sold 200 breads altogether. How many breads had he left?
12. Stick A is 9cm longer than Stick B. 2/3 the length of Stick B is equal to half the length of Stick A. What is the length of Stick B
13. A tank is 1/3 full. After 6 litres of water was added into the tank, it was 7/12 full. Find the capacity of the tank.
14. A tank was 1/10 full of water. After 35 litres of water were added into the tank, it became 3/5 full. How much water was needed to fill up the 2 full tank?
15. Betty had $320 at first. She spent 5/8 of her money at the bookshop and ¼ of it at the supermarket.
a. What fraction of her money was spent?
b. How much had she left?
16. Susie collected 378 beads. 5/9 of them are green and the rest are red and yellow beads. The number of the red beads is thrice as many as the yellow beads.
a. How many more green beads than yellow beads are there?
b. How many red beads should Susie buy so that the number of red beads would be the same as the green beads?
17. Angie, Betty and Cally had $655 altogether. Angie spent 1/3 of her money. Betty spent $25 and Cally spent twice the amount Angie spent. If they had the same amount of money left, how much money did Cally have at first?
18. Some students were given funfair tickets to sell. ½ of them sold their tickets on Monday. 2/5 of the remaining students sold their tickets on Tuesday. The rest of the students sold their tickets on Wednesday. Given that 108 students sold their tickets on Wednesday and each student sold two tickets, how many tickets were sold altogether?
19. Ben has 2/3 as many stickers as Andy. Kyle has 1/6 as many stickers as Ben. If they have 96 stickers in all, how many more stickers does Ben have than Kyle?
20. Ben has $175 more than Calvin. If Calvin has 2/5 as much money as Ben, how much do they have altogether?
Friday, October 23, 2009
Wednesday, September 30, 2009
Term 4 – Problem Solving Practice 3
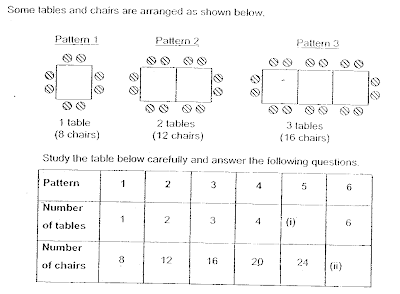
(Pattern Problems – use a table to identify pattern fundamental so as to predict what will come next and what will happen again and again in the same way




(Pattern Problems – use a table to identify pattern fundamental so as to predict what will come next and what will happen again and again in the same way



a. Complete the table above.
b. How many chairs will there be in Pattern 11?
c. Which pattern will have 192 chairs?

Friday, September 25, 2009
Term 4 – Problem Solving Practice 2
(Use Model, branch or unit methods to work out the solution)
1. Tom had ½ the number of marbles Ben had at first. After Ben gave 12 of his marbles to Tom, Tom had 2/3 the number of marbles Ben had. How many marbles did Tom have at first?
2. Eric has 2/3 as many erasers as Felicia. If Eric gives 8 erasers to Felicia, he will have 2/5 as many erasers as Felicia. How many erasers does Eric have at first?
3. Shawn and Roger had an equal number of stickers. After Roger gave 36stickers to Shawn, Shawn had 5 times as many stickers as Roger. How many stickers did Roger have at first?
4. Min had 3/7 of the number of beads that Jake had at first. When Min received 22 beads from Jake, both of them would have an equal number of beads.
a. How many more beads did Jake have than Min at first?
b. How many beads did they have altogether?
5. Three boys Ali, John and David have some marbles. After Ali gave 2/5 of his marbles to David and John gave ¼ of his marbles to David, the three boys have the same number of marbles.
a. Given that Ali has 100 marbles at first, how many marbles does John have at first?
b. During a game, David lost half the number of marbles to Mary. Ali and John each decided to give the same number of marbles to David so that the three of them have an equal number of marbles again. What fraction of the marbles did Ali and John each give to David?
1. Tom had ½ the number of marbles Ben had at first. After Ben gave 12 of his marbles to Tom, Tom had 2/3 the number of marbles Ben had. How many marbles did Tom have at first?
2. Eric has 2/3 as many erasers as Felicia. If Eric gives 8 erasers to Felicia, he will have 2/5 as many erasers as Felicia. How many erasers does Eric have at first?
3. Shawn and Roger had an equal number of stickers. After Roger gave 36stickers to Shawn, Shawn had 5 times as many stickers as Roger. How many stickers did Roger have at first?
4. Min had 3/7 of the number of beads that Jake had at first. When Min received 22 beads from Jake, both of them would have an equal number of beads.
a. How many more beads did Jake have than Min at first?
b. How many beads did they have altogether?
5. Three boys Ali, John and David have some marbles. After Ali gave 2/5 of his marbles to David and John gave ¼ of his marbles to David, the three boys have the same number of marbles.
a. Given that Ali has 100 marbles at first, how many marbles does John have at first?
b. During a game, David lost half the number of marbles to Mary. Ali and John each decided to give the same number of marbles to David so that the three of them have an equal number of marbles again. What fraction of the marbles did Ali and John each give to David?
Wednesday, September 16, 2009
P4 – Term 4 _Problem solving - Time
1. A tour bus drove from Town A to Town C. The bus started at 9.45 a.m.. 4 h and 15 min later, the bus stopped at Town B for half an hour. The tour bus took another 4 h 45 min to reach Town C. When did the tour bus reach Town C?
2. 2. Clarice took 43 sec to solve a maths question. Dawn took 5 sec more than Clarice. Ann took 49 sec to complete it. Bernice was 3 sec faster than Ann. Evelyn took 5 sec more than Bernice. Who was the slowest child and what was her timing?
3. Chee Keong took 35 mins to travel from his home to the stadium to watch a football match. He reached the stadium 20 mins before the match started. If the match lasted 1 h 45 min and ended at 21 30, when did Chee Keong leave his home?
4. Eddie started on his project at 9.30 a.m.. He stopped to take a half-hour break at noon for his lunch. He finished his project at 5.15 p.m.. How long did he take to do his project?
5. Susan took 2h 40 min to complete her homework. Linda started doing her homework at 14 50 and completed it at 16 30. Megan took half the total time taken by both Susan and Linda to do her homework. How long did Megan take to complete her homework? (Express answer in h and min)
2. 2. Clarice took 43 sec to solve a maths question. Dawn took 5 sec more than Clarice. Ann took 49 sec to complete it. Bernice was 3 sec faster than Ann. Evelyn took 5 sec more than Bernice. Who was the slowest child and what was her timing?
3. Chee Keong took 35 mins to travel from his home to the stadium to watch a football match. He reached the stadium 20 mins before the match started. If the match lasted 1 h 45 min and ended at 21 30, when did Chee Keong leave his home?
4. Eddie started on his project at 9.30 a.m.. He stopped to take a half-hour break at noon for his lunch. He finished his project at 5.15 p.m.. How long did he take to do his project?
5. Susan took 2h 40 min to complete her homework. Linda started doing her homework at 14 50 and completed it at 16 30. Megan took half the total time taken by both Susan and Linda to do her homework. How long did Megan take to complete her homework? (Express answer in h and min)
Term 4 - Problem Solving Practice 1
(Use Model, branch or unit methods to work out the solution)
1. In a class of 40 pupils, ½ the number of boys is equal to ¾ the number of girls. How many more boys than girls are there in the class?
2. 0.5 of Ling Yuan’s sum of money is equal to 3/5 of Karen’s sum of money. If Ling Yuan has $24 more than Karen, how much do they have altogether? (Hint : Express the decimal as fraction)
3. In a school, 0.6 of the girls and 0.4 of the boys take part in CCAs. There is an equal number of boys and girls who do not take part in CCAs. If 480 pupils do not take part in CCAs, how many pupils are there in the school?
4. Mrs Tu baked a total of 450 almond cookies and chocolate cookies. After she gave 0.6 of the almond cookies and 0.5 of the chocolate cookies to her friends, she was left with an equal number of almond cookies and chocolate cookies. How many chocolate cookies had she left?
5. Mark and Rosy had a total of $850. After Rosy spent ¼ of her money and Mark spent ½ of his money, both had an equal amount of money left. Find the total amount of money each had at first.
6. Ben had 96 more stickers than Calvin. Calvin used ¾ of his stickers and Ben used 5/6 of his stickers. In the end, Ben had twice as many stickers as Calvin. Find the number of stickers Calvin had at first
7. A bag contained some red marbles and green marbles. 0.2 of the red marbles and 0.6 of the green marbles were removed. In the end, there were half as many red marbles as green marbles. Given that there were 30 more green marbles than red marbles at first, find the number of red marbles in the bag at first.
8. 2/3 of John’s savings is equal to 4/5 of Darren’s savings. John saves $20 more than Darren. How much does Darren save?
9. 2/3 of Sunny’s marbles is equal to 3/5 of Tim’s marbles. If Sunny has 4 marbles less than Tim, how many marbles does Tim have?
10. There are 60 more buttons than marbles in a box. 0.4 of the buttons is equal to 4/7 of the marbles. How many buttons are there in the box? How many buttons and marbles are there in the box altogether?
1. In a class of 40 pupils, ½ the number of boys is equal to ¾ the number of girls. How many more boys than girls are there in the class?
2. 0.5 of Ling Yuan’s sum of money is equal to 3/5 of Karen’s sum of money. If Ling Yuan has $24 more than Karen, how much do they have altogether? (Hint : Express the decimal as fraction)
3. In a school, 0.6 of the girls and 0.4 of the boys take part in CCAs. There is an equal number of boys and girls who do not take part in CCAs. If 480 pupils do not take part in CCAs, how many pupils are there in the school?
4. Mrs Tu baked a total of 450 almond cookies and chocolate cookies. After she gave 0.6 of the almond cookies and 0.5 of the chocolate cookies to her friends, she was left with an equal number of almond cookies and chocolate cookies. How many chocolate cookies had she left?
5. Mark and Rosy had a total of $850. After Rosy spent ¼ of her money and Mark spent ½ of his money, both had an equal amount of money left. Find the total amount of money each had at first.
6. Ben had 96 more stickers than Calvin. Calvin used ¾ of his stickers and Ben used 5/6 of his stickers. In the end, Ben had twice as many stickers as Calvin. Find the number of stickers Calvin had at first
7. A bag contained some red marbles and green marbles. 0.2 of the red marbles and 0.6 of the green marbles were removed. In the end, there were half as many red marbles as green marbles. Given that there were 30 more green marbles than red marbles at first, find the number of red marbles in the bag at first.
8. 2/3 of John’s savings is equal to 4/5 of Darren’s savings. John saves $20 more than Darren. How much does Darren save?
9. 2/3 of Sunny’s marbles is equal to 3/5 of Tim’s marbles. If Sunny has 4 marbles less than Tim, how many marbles does Tim have?
10. There are 60 more buttons than marbles in a box. 0.4 of the buttons is equal to 4/7 of the marbles. How many buttons are there in the box? How many buttons and marbles are there in the box altogether?
P4 _ Term 4 - Wk1 Problem Solving
Have created 2 worksheets this wk. The 1st is the normal weekly problem solving activity using model or the newly introduce alternative problem solving method known as branch and units method.
They are derivatives from the model method but used to simplified problem solving so that the problem is solve much faster and more efficiently.
The 2nd worksheet focus on topics Time .... these questions appear in the section C of past-year top school SA2 exam.
Have fun
They are derivatives from the model method but used to simplified problem solving so that the problem is solve much faster and more efficiently.
The 2nd worksheet focus on topics Time .... these questions appear in the section C of past-year top school SA2 exam.
Have fun
Subscribe to:
Posts (Atom)